Đường cong đại số
Trong toán học, đường cong phẳng đại số affin là tập nghiệm của đa thức hai biến. đường cong phẳng đại số xạ ảnh là tập nghiệm trong mặt phẳng xạ ảnh của đa thức thuần nhất trong ba biến. đường cong phẳng đại số affin có thể chuyển thành đường cong phẳng đại số xạ ảnh bằng cách thuần nhất hoá đa thức của nó. Ngược lại, đường cong phẳng đại số xạ ảnh của phương trình thuần nhất h(x, y, t) = 0 có thể giới hạn về đường cong phẳng đại số affin dưới phương trình h(x, y, 1) = 0. Hai phép biến đổi này là nghịch đảo của nhau; do đó, ta có thể dùng chung thuật ngữ đường cong phẳng đại số mà không cần phải quan tâm tới nó là xạ ảnh hay affin.
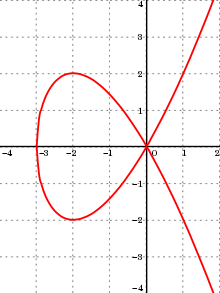
Tổng quát hơn, đường cong đại số là đa tạp đại số có chiều bằng một. Hoặc nói một cách tương đương, đường cong đại số là đa tạp đại số tương đương song hữu tỉ với một đường cong phẳng đại số nào đó. Nếu đường cong đó nằm trong không gian affin hoặc không gian xạ ảnh, ta có thể dùng phép chiếu để tìm ra tương đương song hữu tỷ đó.
Các tương đương song hữu tỉ giúp rút gọn nghiên cứu các đường cong đại số về các đường cong phẳng đại số. Tuy nhiên, vẫn có một số tính chất không được giữ trong tương đương song hữu tỉ và do đó phải được nghiên cứu trên đường không phẳng. Một trong số các tính chất đó là bậc và độ trơn. Ví dụ như, tồn tại các đường con trơn có giống bằng 0 và bậc lớn hơn hai nhưng phép chiếu trên mặt phẳng của các đường cong đó có các điểm kỳ dị (xem công thức giống-bậc).
Đường không phẳng còn được gọi là đường không gian hay đường xiên.
Trong hình học Euclid
sửaĐường cong đại số trong mặt phẳng Euclid là tập các điểm mà toạ độ của nó là nghiệm của phương trình đa thức hai biến p(x, y) = 0. Phương trình này còn được gọi là phương trình ẩn của đường cong.
Một trong những bài toán đầu tiên khi xét đường cong đại số là xác định hình dạng của đồ thị của nó rồi vẽ. Bài toán này không dễ như khi vẽ đồ thị của hàm số khi các giá trị y có thể dễ dàng tính từ nhiều giá trị của x. Song ta có thể dựa vào định nghĩa phương trình là đa thức để tìm ra một số cấu trúc giải quyết bài toán.
Mọi đường cong đại số đều có thể phân tách duy nhất thành hữu hạn số các cung đơn điệu và trơn (còn được gọi là các nhánh), đôi khi được nối với nhau bằng các điểm được gọi "điểm nổi bật", và có thể hữu hạn số điểm cô lập khác. Cung đơn điệu và trơn là đồ thị của hàm trơn được xác định và đơn điệu trên một khoảng mở của trục x. Theo mỗi hướng, cung đó hoặc không bị chặn (thường hay gọi là cung vô hạn) hoặc có điểm mút là điểm kỳ dị (được định nghĩa bên dưới) hoặc là điểm có đường tiếp tuyến song song với một trong hai trục toạ độ.
Lấy ví dụ, xét đường cong bậc ba Tschirnhausen, có hai cung vô hạn lấy điểm (0,0) là điểm mút. Điểm (0, 0) này là điểm kỳ dị duy nhất của đường cong đó. Trong đường cong còn có thêm hai cung cũng có điểm này làm điểm mút và điểm mút còn lại có đường tiếp tuyến ngang. Ngoài ram có hai cung khác trong đó mỗi điểm mút đó có một điểm mút có tiếp tuyến ngang và một điểm mút có tiếp tuyến dọc. Ngược lại, sóng sin không phải đường cong đại số bởi nó có vô hạn số cung đơn điệu.
Để vẽ đường cong đại số, ta cần để ý tới các điểm nổi bật và các đường tiếp tuyến của nó, các nhánh vô hạn và tiệm cận của chúng (nếu có) và cách mà các cung nối với nhau. Ngoài ra cũng có thể xét các điểm uốn làm điểm nổi bật. Khi vẽ tất cả các thông tin này ra giấy, thường thì có thể hình dung ngay hình dạng của đường cong. Nếu vẫn chưa xác định được thì ta chỉ cần thêm vài điểm và một số tiếp tuyến để có thể hình dung ra đường cong.
Các phương pháp để tính các điểm nổi bật và các tiếp tuyến của nó được đề cập dưới đây.
Đường xạ ảnh phẳng
sửaĐể thuận lợi, ta thường xét các đường cong trong không gian xạ ảnh. Đường cong đại số trong mặt phẳng xạ ảnh hay còn gọi là đường xạ ảnh phẳng là tập các điểm trong mặt phẳng xạ ảnh có các toạ độ xạ ảnh là nghiệm của đa thức thuần nhất ba biến P(x, y, z).
Mọi đường cong đại số affin của phương trình p(x, y) = 0 có thể chuyển thành thành đường cong xạ ảnh của phương trình trong đó là kết quả thuần nhất hoá p. Ngược lại, nếu P(x, y, z) = 0 là phương trình thuần nhất của đường cong xạ ảnh, thì P(x, y, 1) = 0 là phương trình của đường cong affin chứa các điểm của đường con xạ ảnh có toạ độ xạ ảnh thứ ba khác không. Hai phép thực hiện này nghịch đảo cho nhau bởi và, nếu p được định nghĩa bởi , thì ngay khi đa thức thuần nhất P không chia hết cho z.
Lấy ví dụ, đường cong xạ ảnh của phương trình x2 + y2 − z2 là hoàn thiện xạ ảnh của đường tròn đơn vị của phương trình x2 + y2 − 1 = 0.
Từ đây cho thấy rằng đường cong affin và đường xạ ảnh lấy từ là cùng một đường cong, hay nói một cách chuẩn xác hơn, đường cong affin là một phần của đường cong xạ ảnh nhưng đủ lớn để có thể định nghĩa hoàn toàn "toàn bộ" đường cong.
Đường xạ ảnh thường được nghiên cứu riêng. Nó thường được áp dụng khi nghiên cứu đường cong affin. Lấy ví dụ, nếu p(x, y) là đa thức định nghĩa đường cong affin, bên cạnh đạo hàm riêng và , ta cũng có thể xét đạo hàm tại vô cực
Lấy ví dụ, phương trình của đường tiếp tuyến của đường cong affine có phương trình p(x, y) = 0 tại điểm (a, b) là
Các điểm nổi bật của đường cong phẳng
sửaỞ đây, ta sẽ xét đường cong đại số phẳng định nghĩa bởi đa thức hai biến p(x, y) và dạng xạ ảnh của nó, định theo phương trình thuần nhất của p.
Giao với một đường thẳng
sửaGiao với các trục toạ độ và các tiệm cận rất có ích cho việc vẽ đường cong. Giao với một đường song song với trục toạ độ cho phép ta tìm ra ít nhất một điểm thuộc mỗi nhánh của đường cong. Nếu có một thuật toán tìm nghiệm hiệu quả, thì sẽ cho phép ta có thể vẽ đường cong bằng cách vẽ các giao điểm với tất cả các đường song song với trục y và chạy qua mỗi pixel trên trục x.
Nếu đa thức định nghĩa đường cong có bậc d, thì mọi đường thẳng sẽ cắt đường cong tối đa d điểm. Định lý Bézout khẳng định số giao điểm bằng d nếu các điểm được tìm trong không gian xạ ảnh trên trường đóng đại số (ví dụ như số phức), và được đếm cùng số bội. Phương pháp tính sau chứng minh định lý này trong trường hợp đơn giản.
Để tính giao của đường cong định nghĩa bởi đa thức p với đường thẳng có phương trình ax+by+c = 0, ta cần giải phương trình đường thẳng cho x (hoặc cho y nếu a = 0). Thay kết quả vào p, ta đường phương trình một biến q(y) = 0 (hay q(x) = 0, nếu phương trình đường thẳng được giải theo y), mỗi nghiệm này đều là một trong hai toạ độ của giao điểm. Toạ độ còn lại sẽ được suy từ phương trình đường thẳng. Số bội của giao điểm là số bội của nghiệm tương ứng. Có giao điểm tại vô cực nếu bậc của q nhỏ hơn bậc của p; khi đó số bội của giao điểm tại vô cực sẽ bằng hiệu giữa bậc của p và q.
Tiếp tuyến tại một điểm
sửaTiếp tuyến tại điểm (a, b) của đường cong là đường thẳng có phương trình , giống như mọi đường cong khả vi định nghĩa theo phương trình ẩn. Trong trường hợp đa thức, có một công thức khác đơn giản hơn và đối xứng hơn như sau:
trong đó là đạo hàm tại vô cực. Tương đương giữa hai phương trình được chứng minh bằng cách áp dụng định lý thuần nhất của Euler cho P.
Nếu , tiếp tuyến sẽ không xác định được và điểm đó sẽ thành điểm kỳ dị.
Ta có thể lập tức mở rộng sang trường hợp xạ ảnh: Phương trình tiếp tuyến của điểm có toạ độ xạ ảnh (a:b:c) của đường cong xạ ảnh với phương trình P(x, y, z) = 0 là
là các điểm kỳ dị của đường cong đó là các điểm thoả mãn
(Điều kiện P(a, b, c) = 0 suy ra từ các điều kiện này, theo định lý thuần nhất hàm của Euler.)
Tiệm cận
sửaMọi nhánh vô hạn của đường cong đại số đều tương ứng với một điểm vô hạn trên đường cong, và điểm đó là điểm của hoàn thiện xạ ảnh của đường cong không nằm trong dạng affin. Tiệm cận tương ứng là tiếp tuyến của đường cong tại điểm đó. Ta có thể áp dụng công thức chung của tiếp tuyến cho đường cong xạ ảnh, nhưng ở đây sẽ có công thức riêng.
Đầu tiên ta phân tách đa thức p thành các đa thức thuần nhất nhỏ hơn , trong đó pi là tổng của các đa thức monic của p có bậc i. Từ đây ta sẽ suy ra rằng và
Điểm tại vô cực tại đường cong là nghiệm của p dưới dạng (a, b, 0). hoặc tương đương, (a, b) là nghiệm của pd. Áp dụng định lý cơ bản của đại số sẽ suy ra rằng, trên trường đóng đại số (thường sẽ là trường số phức) pd sẽ phân tích thành tích của phần tử tuyến tính. Mỗi phần tử sẽ định nghĩa một điểm tại vô cực của đường cong: nếu bx − ay là một trong những phần tử đó, thì nó sẽ định nghĩa điểm tại vô cực (a, b, 0). Trên các số thực, pd phân tích thành các phần tử tuyến tính và phần tử toàn phương. Các phần tử toán phương bất khả quy sẽ định nghĩa các điểm không thực tại vô cực, còn các điểm thực sẽ được lấy từ các phần tử tuyến tính. Nếu (a, b, 0) là điểm tại vô cực của của đường cong, có thể nói (a, b) là hướng tiệm cận. Đặt q = pd, phương trình của tiệm cận tương ứng là
Nếu và tiệm cận là đường tại vô cực, và trong trường hợp số thực, đường cong có nhánh giống với parabol. Trong trường hợp này ta có thể nói đường có nhánh parabol. Nếu đường cong sẽ có điểm kỳ dị tại vô cực và có thể có nhiều tiệm cận. Các điểm đó có thể được tìm qua phương pháp tìm mặt nón tiếp tuyến của điểm kỳ dị.
Điểm kỳ dị
sửaCác điểm kỳ dị của đường cong có bậc d định nghĩa bởi đa thức p(x,y) có bậc d là nghiệm của hệ phương trình sau: Trong trường đặc số không, hệ này tương đương với trong đó, dùng ký hiệu của nội dung trước, Hai hệ này tương đương nhau theo Định lý thuần nhất hàm của Euler. Hệ sau có ưu điểm ở chỗ đa thức thứ ba có bậc d-1 thay vì d.
Tương tự, đối với đường cong xạ ảnh định nghĩa bởi đa thức thuần nhất P(x,y,z) bậc d, các điểm kỳ dị là nghiệm của phương trình sau với toạ độ thuần nhất. (Nếu đặc số dương thì phải thêm phương trình vào trong hệ.)
Điều này cho thấy số điểm kỳ dị là hữu hạn miễn sao p(x,y) hoặc P(x,y,z) không bình phương. Từ định lý Bézout suy ra số các điểm kỳ dị tối đa là (d−1)2, nhưng cận này quá lớn bởi hệ phương trình bị xác định quá mức. Nếu cho phép các đa thức khả quy, cận chuẩn hơn là d(d−1)/2, và giá trị này được chạm tới khi các đa thức phân tích thành các phần tử tuyến tính, nghĩa là nếu đường cong là hợp của d đường thẳng. Đối với các đa thức và đường cong bất khả quy, số các điểm kỳ dị tối đa là (d−1)(d−2)/2, theo cách thức tính giống theo số kỳ dị. Giá trị cực đại được chạm tới bởi các đường cong có giống hai mà tất cả kỳ dị của nó đều có số bội hai và tiếp tuyến phân biệt.
Phương trình tiếp tuyến tại điểm kỳ dị được đưa bởi phần thuần nhất khác không có bậc nhỏ nhất trong chuỗi Taylor của đa thức tại điểm kỳ dị. Khi ta đổi toạ độ để đặt điểm kỳ dị tại gốc toạ độ, phương trình của các tiếp tuyến tại điểm kỳ dị sẽ là phần thuần nhất khác không có bậc nhỏ nhất của đa thức, và số bội của điểm kỳ dị là bậc của phần thuần nhất đó.
Cấu trúc giải tích
sửaNghiên cứu cấu trúc giải tích của đường cong đại số trong lân cận của điểm kỳ dị cho thêm thông tin chính xác về tô pô của các điểm kỳ dị. Thậm chí, khi gần điểm kỳ dị, đường cong đại số trở thành hợp của hữu hạn số nhánh chỉ giao với nhau tại điểm kỳ dị và có hình dạng giống với điểm lùi hoặc là đường cong trơn.
Gần điểm chính quy, một trong các toạ độ của đường cong có thể biểu diễn thành hàm giải tích của các toạ độ khác. Đây là hệ quả của định lý phương trình ẩn, và suy ra rằng đường cong sẽ trơn khi gần điểm đó. Khi gần điểm kỳ dị, bài toán trở nên phức tạp hơn và có bao gồm sử dụng chuỗi Puiseux, đưa ra các phương trình tham số của các nhánh.
Để mô tả điểm kỳ dị, ta nên tịnh tiến các điểm kỳ dị về gốc toạ độ. Tức là đổi toạ độ các biến về trong đó là toạ độ các điểm kỳ dị. Trong nội dung sau, các điểm kỳ dị được xét sẽ được ngầm trước là nằm ở gốc toạ độ.
Phương trình của đường con đại số là trong đó f là đa thức với biến x và y. Đa thức có thể coi là đa thức trong biến y, với hệ số trong trường đóng đại số của chuỗi Puiseux trong x. Do đó f có thể phân tích thành các phần tử dưới dạng trong đó P là chuỗi Puiseux. Các phần tử khác nhau phân biệt nếu f là đa thức bất khả quy, bởi từ đây suy ra f không bình phương, tính chất này không phụ thuộc vào trường của các hệ số.
Chuỗi Puiseux ở đây có dạng sau trong đó d là số nguyên dương, và là số nguyên tuỳ ý mặc định trước ở đây là dương bởi ta chỉ xét các nhánh đi qua gốc toạ độ. Không mất tính tổng quát, ta giả sử rằng d nguyên tố cùng nhau với ước chung lớn nhất của n sao cho (nếu không thì ta có thể chọn mẫu số chung nhỏ hơn cho các số mũ).
Gọi là căn đơn vị nguyên thuỷ thứ d.Nếu chuỗi Puiseux ở trên xuất hiện trong phân tích của , thì chuỗi d sau cũng xuất hiện trong phân tích đó (đây là hệ quả của lý thuyết Galois). Chuỗi d này được gọi là liên hợp đại số, và được coi là một nhánh của đường cong, với chỉ số rẽ nhánh d.
Trong trường hợp đường cong thực, tức là đường cong định nghĩa bởi đa thức có các hệ số thực, có ba trường hợp có thể xảy ra. Nếu không có nào có hệ số thực, thì ta sẽ có một nhánh không thực. Nếu một số trong có hệ số thực, thì ta có thể chọn một trong số đó làm . Nếu d lẻ, thì mọi giá trị thực của x sẽ tính ra giá trị thực của , và ta sẽ có một nhánh trông chính quy, mặc dù nó kỳ dị nếu d > 1. Nếu d chẵn, thì và có giá trị thực, nhưng chỉ đối với x ≥ 0. Trong trường hợp này, nhánh thực sẽ trông giống như hình chỏm.
Lấy ví dụ, hình chỏm thường sẽ chỉ có một nhánh. Nếu nó được định nghĩa bởi phương trình thì phân tích của nó sẽ là chỉ số rẽ nhánh bằng 2, hai phần tử này đều thực và đều định nghĩa một nửa nhánh. Nếu hình được quay, phương trình của nó trở thành và phân tích của nó là với (hệ số chưa được giản hoá về j để cho thấy định nghĩa trên của ). Ở đây chỉ số rẽ nhánh là 3, và chỉ có một phần tử trong đây là thực; điều này cho thấy rằng. trong trường hợp ban đầu, cả hai phần tử đều phải định nghĩa cùng một nhánh.
Đường cong đại số không phẳng
sửaĐường cong đại số là đa tạp đại số có chiều bằng một. Điều này suy ra rằng đường cong affin trong không gian affin có chiều n được định nghĩa bởi ít nhất n−1 đa thức n biến. Để định nghĩa một đường cong, các đa thức này phải sinh ra ideal nguyên tố có số chiều Krull bằng 1. Điều kiện này không dễ để kiểm tra, do đó các nhà toán học thường dùng cách sau để biểu diễn đường cong không phẳng.
Gọi là n đa thức trong hai biến x1 and x2 sao cho f bất khả quy. Các điểm trong không gian affin chiều n có toạ độ thoả mãn các phương trình và bất phương trình sau
là tất cả các điểm của một đường cong đại số trong đó đã bỏ đi hữu hạn số điểm. Đường cong này được định nghĩa bởi hệ các phần tử sinh của ideal của các đa thức h sao cho tồn tại số nguyên k thoả mãn thuộc về ideal sinh bởi . Biểu diễn này có tương đương song hữu tỉ giữa đường cong và đường cong phẳng định nghĩa bởi f. Mọi đường cong đại số có thể biểu diễn theo cách này. Tuy nhiên, ta cần thay đổi tuyến tính các biến để gần như chiếu nội xạ lên hai biến đầu tiên. Khi cần phải thay đổi các biến, thì gần như mọi thay đổi đều có lợi khi nó được định nghĩa trên trường vô hạn.
Biểu diễn này cho phép các nhà toán học suy ra bất kỳ tính chất của đường cong đại số không phẳng, bao gồm biểu diễn đồ thị của nó từ các tính chất của phép chiếu trên mặt phẳng.
Đối với đường cong được định nghĩa bởi các phương trình ẩn của nó, biểu diễn trên có thể suy ra được từ cơ sở Gröbner cho xếp thứ tự khối sao cho khối có các biến nhỏ hơn là (x1, x2). Đa thức f là đa thức duy nhất cơ sở chỉ phụ thuộc vào x1 và x2. Các phân thức gi/g0 thu về được bằng cách chọn từ i = 3, ..., n, một đa thức trong cơ sở mà tuyến tính trong xi và chỉ phụ thuộc trên x1, x2 và xi.Nếu không thể chọn ra được đa thức nào, thì có nghĩa là phương trình đó định nghĩa tập đại số không phải đa tạp, hoặc đa tạp đó không có chiều bằng một, hoặc ta phải đổi toạ độ. Trường hợp cuối xảy ra khi f tồn tại và duy nhất, ngoài ra trong i = 3, …, n, tồn tại các đa thức mà đơn thức đứng đầu chỉ phụ thuộc trên x1, x2 và xi.
Trường hàm đại số
sửaNghiên cứu các đường cong đại số có thể rút gọn sang nghiên cứu các đường cong bất khả quy: tức là các đường cong không thể viết thành hợp của đường cong nhỏ hơn. Xét xê xích tương đương song hữu tỉ, các đường cong bất khả quy trên trường F tương đương phạm trù với trường hàm đại số trong một biến trên F. Trường hàm đại số là mở rộng trường K của F chứa phần tử x siêu việt trên F, và sao cho K là mở rộng đại số hữu hạn của F(x) (F(x) là trường của các hàm hữu tỉ có biến x trên F).
Lấy ví dụ, xét trường C của các số phức, trên đó ta có thể định nghĩa trường hàm số C(x) của các hàm hữu tỉ trong C. Nếu y2 = x3 − x − 1, thì trường C(x, y) là trường hàm elliptic. Phần tử x không được xác định duy nhất; bởi trường đó còn có thể coi là mở rộng C(y).Đường cong đại số tương ứng với trường hàm số là tập các điểm (x, y) trong C2 thoả mãn y2 = x3 − x − 1.
Nếu trường F không đóng đại số, thì góc nhìn từ trườh hàm số tổng quát hơn góc nhìn tử luỹ tích các điểm, bởi khi đó ta bao gồm cả các "đường cong" không có điểm nào trên chúng. Lấy ví dụ, nếu trường gốc F là trường R của các số thực, thì x2 + y2 = −1 định nghĩa một trường mở rộng đại số của R(x), nhưng đường cong tương khi được xét là tập con là R2 không chứa điểm nào. Phương trình x2 + y2 = −1 có định nghĩa đường cong đại số bất khả quy trên R theo góc nhìn từ lược đồ ,(là lược đồ nguyên, đã tách và một chiều của kiểu hữu hạn trên R). Theo cách hiểu này, tương ứng một-một giữa các đường cong đại số bất khả quy trên F (xê xích song hửu tỉ) và các trường hàm đại số trên F thường được thoả mãn.
Hai đường con có thể tương đương song hữu tỉ với nhau (tức là có trường hàm đại số đẳng cấu với nhau) mà không cần đẳng cấu với nhau. Bài toán trở nên dễ hơn khi xét các đường cong không kỳ dị, tức là các đường không điểm kỳ dị nào. Hai đường cong xạ ảnh không kỳ dị trên một trường đẳng cấu với nhau khi và chỉ khi trường hàm số của nó đẳng cấu với nhau.
Định lý Tsen phát biểu về trường hàm đại số của đường cong đại số trên trường đóng đại số.
Đường cong phức và mặt phẳng thực
sửaĐường cong đại số xạ ảnh phức trong không gian xạ ảnh phức n chiều CPn.Không gian này có số chiều phức bằng với n, nhưng số chiều tô pô của nó khi xét là đa tạp thực là 2n, và là không gian compact, liên thông, và định hướng được. Đường cong đại số tương tự trên C có số chiều tô pô bằng hai; Nói cách khác, nó là một mặt phẳng.
Số giống tô pô, tức là số tay cầm hay số lỗ vòng, bằng với số giống hình học của đa đường cong đại số được tính bằng đại số. Nói chung là, nếu xét hình chiếu trên mặt phẳng của đường cong không kỳ dị bậc d và chỉ các điểm kỳ dị thường (tức các điểm kỳ dị có số bội hai với tiếp tuyến phân biệt), thì số giống là (d − 1)(d − 2)/2 − k, trong đó k là số điểm kỳ dị loại trên.
Xem thêm
sửaHình học đại số cổ điển
sửaHình học đại số hiện đại
sửaHình học của mặt Riemann
sửaChú thích
sửaTham khảo
sửa- Brieskorn, Egbert; Knörrer, Horst (2013). Plane Algebraic Curves. Stillwell, John biên dịch. Birkhäuser. ISBN 978-3-0348-5097-1.
- Chevalley, Claude (1951). Introduction to the Theory of Algebraic Functions of One Variable. Mathematical surveys. 6. American Mathematical Society. ISBN 978-0-8218-1506-9.
- Coolidge, Julian L. (2004) [1931]. A Treatise on Algebraic Plane Curves. Dover. ISBN 978-0-486-49576-7.
- Farkas, H. M.; Kra, I. (2012) [1980]. Riemann Surfaces. Graduate Texts in Mathematics. 71. Springer. ISBN 978-1-4684-9930-8.
- Fulton, William (1989). Algebraic Curves: An Introduction to Algebraic Geometry. Mathematics lecture note series. 30 (ấn bản thứ 3). Addison-Wesley. ISBN 978-0-201-51010-2.
- Gibson, C.G. (1998). Elementary Geometry of Algebraic Curves: An Undergraduate Introduction. Cambridge University Press. ISBN 978-0-521-64641-3.
- Griffiths, Phillip A. (1985). Introduction to Algebraic Curves. Translation of Mathematical Monographs. 70 (ấn bản thứ 3). American Mathematical Society. ISBN 9780821845370.
- Hartshorne, Robin (2013) [1977]. Algebraic Geometry. Graduate Texts in Mathematics. 52. Springer. ISBN 978-1-4757-3849-0.
- Iitaka, Shigeru (2011) [1982]. Algebraic Geometry: An Introduction to Birational Geometry of Algebraic Varieties. Graduate Texts in Mathematics. 76. Springer New York. ISBN 978-1-4613-8121-1.
- Milnor, John (1968). Singular Points of Complex Hypersurfaces. Princeton University Press. ISBN 0-691-08065-8.
- Serre, Jean-Pierre (2012) [1988]. Algebraic Groups and Class Fields. Graduate Texts in Mathematics. 117. Springer. ISBN 978-1-4612-1035-1.
- Kötter, Ernst (1887). “Grundzüge einer rein geometrischen Theorie der algebraischen ebenen Curven” [Fundamentals of a purely geometrical theory of algebraic plane curves]. Transactions of the Royal Academy of Berlin. — gained the 1886 Academy prize[1]
Bản mẫu:Algebraic curves navbox Bản mẫu:Curves
- ^ Norman Fraser (tháng 2 năm 1888). “Kötter's synthetic geometry of algebraic curves”. Proceedings of the Edinburgh Mathematical Society. 7: 46–61, See p. 46.