Sắp xếp nổi bọt

Sắp xếp nổi bọt (tiếng Anh: bubble sort) là một thuật toán sắp xếp đơn giản, với thao tác cơ bản là so sánh hai phần tử kề nhau, nếu chúng chưa đứng đúng thứ tự thì đổi chỗ (swap). Có thể tiến hành từ trên xuống (bên trái sang) hoặc từ dưới lên (bên phải sang). Sắp xếp nổi bọt còn có tên là sắp xếp bằng so sánh trực tiếp. Nó sử dụng phép so sánh các phần tử nên là một giải thuật sắp xếp kiểu so sánh.

Sắp xếp nổi bọt

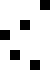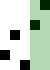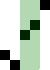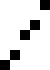Phân loại	Giải thuật sắp xếp
Cấu trúc dữ liệu	Ngẫu nhiên
Hiệu suất trường hợp tệ nhất	Trung bình $O(n^{2})$
Độ phức tạp không gian trường hợp tệ nhất	Không tốn thêm vùng nhớ
Tối ưu	Không

Một ví dụ về sắp xếp nổi bọt. Bắt đầu từ vị trí đầu tiên của danh sách (bên trái), so sánh các cặp số với nhau, nếu không đúng thứ tự nhỏ-lớn thì đảo vị trí. Sau khi chạy tới cuối danh sách, tiếp tục chạy lại từ vị trí đầu danh sách cho đến khi hoàn thành so sánh và đảo vị trí.

Sắp xếp nổi bọt màu đã chỉnh sửa

Giải thuật

Sắp xếp từ trên xuống

Giả sử dãy cần sắp xếp có n phần tử. Khi tiến hành từ trên xuống, ta so sánh hai phần tử đầu, nếu phần tử đứng trước lớn hơn phần tử đứng sau thì đổi chỗ chúng cho nhau. Tiếp tục làm như vậy với cặp phần tử thứ hai và thứ ba và tiếp tục cho đến cuối tập hợp dữ liệu, nghĩa là so sánh (và đổi chỗ nếu cần) phần tử thứ n-1 với phần tử thứ n. Sau bước này phần tử cuối cùng chính là phần tử lớn nhất của dãy.

Sau đó, quay lại so sánh (và đổi chố nếu cần) hai phần tử đầu cho đến khi gặp phần tử thứ n-2....

Ghi chú: Nếu trong một lần duyệt, không phải đổi chỗ bất cứ cặp phần tử nào thì danh sách đã được sắp xếp xong.

Sắp xếp từ dưới lên

Sắp xếp từ dưới lên so sánh (và đổi chỗ nếu cần) bắt đầu từ việc so sánh cặp phần tử thứ n-1 và n. Tiếp theo là so sánh cặp phần tử thứ n-2 và n-1,... cho đến khi so sánh và đổi chỗ cặp phần tử thứ nhất và thứ hai. Sau bước này phần tử nhỏ nhất đã được nổi lên vị trí trên cùng (nó giống như hình ảnh của các "bọt" khí nhẹ hơn được nổi lên trên). Tiếp theo tiến hành với các phần tử từ thứ 2 đến thứ nm.

Mã giả

Sắp xếp từ trên xuống

procedure bubble_sort1(list L, number n) //n=listsize
  For number i from  n downto 2 
    for number j from 1 to (i - 1)
      if L[j] > L[j + 1] //nếu chúng không đúng thứ tự
        swap(L[j], L[j + 1]) //đổi chỗ chúng cho nhau
      endif
    endfor
   endfor
endprocedure

Sắp xếp từ dưới lên

procedure bubble_sort2(list L, number n) //n=listsize
  For number i from 1 to n-1 
    for number j from n-1 downto i
      if L[j] > L[j + 1] //nếu chúng không đúng thứ tự
        swap(L[j], L[j + 1]) //đổi chỗ chúng cho nhau
      endif
    endfor
   endfor
endprocedure

Giảm bớt vòng duyệt

Nếu trong một lần duyệt nào đó với một i cố định khi vòng lặp j kết thúc mà không cần phải đổi chỗ cặp phần tử nào, nghĩa là mọi cặp phần tử kề nhau đã đứng đúng thứ tự thì dãy đã được sắp xếp và không cần tiến hành vòng lặp tiếp theo. Do đó có thể dùng một cờ để kiểm soát việc này. Ta có một đoạn mã giả của thuật toán nổi bọt như sau:

procedure bubble_sort3(list L, number n)
  i:= n
  while i > 1 do
    has_swapped:= 0 //khởi tạo lại giá trị cờ
    for number j from 1 to (i - 1)
      if L[j] > L[j + 1] //nếu chúng không đúng thứ tự
        swap(L[j], L[j + 1]) //đổi chỗ chúng cho nhau
        has_swapped:= 1 //có đổi chỗ ít nhất một lần, danh sách chưa sắp xếp xong
      endif
    endfor  
    if has_swapped = 0 //nếu không có lần đổi chỗ nào, danh sách đã sắp xếp xong
      exit
     else //nếu có ít nhất một lần đổi chỗ, danh sách chưa sắp xếp xong
      i = i - 1
    endif
  enddo
endprocedure

Ghi chú: Cũng có thể không cần dùng đến biến i, khi đó mỗi lần kiểm tra đều phải duyệt từ đầu đến cuối dãy.

Thời gian tính

Với mỗi i = 1,2,..,n-1 ta cần i phép so sánh. Do đó số nhiều nhất các lần so sánh và đổi chỗ trong giải thuật là

$(n-1)+(n-2)+...+2+1={\frac {(n-1)n}{2}}$

Do đó độ phức tạp của giải thuật cỡ O($n^{2}$).

Mã thật ví dụ

Viết bằng Pascal

var a: array[1..1000] of integer;
    n, i: integer;

procedure BubbleSort;
    var
        i, j, tmp: integer;
        
    begin
        for i:= 1 to n - 1 do
            for j:= i + 1 to n do
                if a[i] < a[j] then
                    begin
                        tmp:= a[i];
                        a[i]:= a[j];
                        a[j]:= tmp;
                    end;
    end;
    
BEGIN
    readln(n);
    
    for i:= 1 to n do
        readln(a[i]);
        
    BubbleSort;
    
    for i:= 1 to n do
        write(a[i], ' ');
        
    readln
END.

Viết bằng Java

    private static void bubbleSort(int[] unsortedArray, int length) {
        int temp, counter, index;
        
        for(counter=0; counter<length-1; counter++) { //Loop once for each element in the array.
            for(index=0; index<length-1-counter; index++) { //Once for each element, minus the counter.
                if(unsortedArray[index] > unsortedArray[index+1]) { //Test if need a swap or not.
                    temp = unsortedArray[index]; //These three lines just swap the two elements:
                    unsortedArray[index] = unsortedArray[index+1];
                    unsortedArray[index+1] = temp;
                }
            }
        }
    }

Viết bằng C++

#include <bits/stdc++.h> 
using namespace std; 
long long a[N], n;//Thay N là số phần tử trong mảng 

template<class T,class Cmp = less<T> >
void bubblesort(T *L,T *R,Cmp ss= less<T>())  //sap *L,*(L+1)...*(R-1)
{
    for(T *i=L;i<R;i++)
        for(T *j=R-1;j>L;j--)
            if(ss(*j,*(j-1))) 
       swap(*j,*(j-1));
}
int main() { 
    cin>>n; 
    for(int i=1; i<=n;i++) 
    cin>>a[i]; 
    bubblesort(a+1,a+n+1); 
    for(int i=1; i<=n;i++) 
    cout<<a[i]<<" "; 
}

Viết bằng PHP

$arr=array(1,5,7,8,9,10,2,3,6);
function s($a,$b){
    if($a==$b){
        return 1;
    }
    if($a<$b){
    return 1;
    }else{
    return -1;
    }
}
usort($arr,'s');
print_r($arr);
exit();

other code

$arr = [...];
$arr_count = count($arr);

//loop
for ($i = 0; $i < $arr_count; $i++)
{
    for ($j = 1; $j < $arr_count - $i; $j++)
    {
        if ($arr[$j-1] > $arr[$j])
        {
            $tmp = $arr[$j-1];
            $arr[$j-1] = $arr[$j];
            $arr[$j] = $tmp;
        }
    }
}

for($i=0;$i<$arr_count;$i++){
    echo $arr[$i]."<br>";
}

Viết bằng Python

list = []
list_final = []
num = int(input("how many number you want to add?\n"))
for i in range(num) :
    number = int(input("adding numbers"))
    list.append(number)
    if list[i] not in list_final :
        list_final.append(list[i])#if list exits the same number many timnes , it will delete and make the list_final 
for j in range(len(list_final)):
    for k in range(j):
        if list_final[j] < list_final[k]:#compare numbers in the list
            tmp = list_final[j]
            list_final[j] = list_final[k]
            list_final[k] = tmp
print(list_final)

Xem thêm

• Sắp xếp chèn
• Sắp xếp chọn
• Sắp xếp vun đống
• Sắp xếp nhanh
• Sắp xếp trộn