Nomogram
Nomograph (còn gọi là bảng đồ, biểu đồ căn chỉnh hoặc abac) là một thiết bị tính toán đồ họa, một biểu đồ hai chiều được thiết kế để cho phép tính toán xấp xỉ đồ họa của một hàm toán học. Tên gọi "Nomograph" có nguồn gốc từ tiếng Hy Lạp: nomos νόμος, "luật" và grammē γραμμή, "đường thẳng"). Lĩnh vực nomography được phát minh vào năm 1884 bởi kỹ sư người Pháp Philbert Maurice d'Ocagne (1862-1938) và đã được sử dụng rộng rãi trong nhiều năm để cung cấp cho người kỹ sư các tính toán đồ họa nhanh chóng của các công thức phức tạp với độ chính xác thực tế. Nomogram sử dụng hệ tọa độ song song được d'Ocagne phát minh thay vì hệ tọa độ Descartes tiêu chuẩn.
Một Nomogram bao gồm một bộ n các thang đo, một cho mỗi biến trong phương trình. Bằng cách biết giá trị của n-1 biến, giá trị của biến chưa biết có thể được tìm ra, hoặc bằng cách cố định giá trị của một số biến, mối quan hệ giữa các biến chưa cố định có thể được nghiên cứu. Kết quả được thu về bằng cách đặt một cạnh thẳng qua các giá trị đã biết trên các thang đo và đọc giá trị chưa biết từ vị trí nó cắt thang đo cho biến số đó. Đường thẳng ảo hoặc được vẽ bằng cạnh thẳng được gọi là đường chỉ số (index line) hoặc đường thẳng phương tuyến isopleth.
Các Nomogram phát triển mạnh mẽ trong nhiều ngữ cảnh khác nhau khoảng 75 năm qua vì chúng cho phép tính toán nhanh chóng và chính xác trước thời kỳ của máy tính cầm tay. Bảng đồ cho ra kết quả rất nhanh chóng và đáng tin cậy chỉ bằng cách vẽ một hoặc nhiều đường thẳng. Người dùng không cần phải biết cách giải phương trình đại số, tìm kiếm dữ liệu trong bảng, sử dụng thước trượt, hoặc thay thế số vào phương trình để thu về kết quả. Người dùng thậm chí chẳng cần phải biết phương trình cơ bản mà bảng đồ đại diện. Ngoài ra, bảng đồ được tích hợp một cách tự nhiên kiến thức miền ẩn hoặc rõ ràng vào thiết kế của chúng. Ví dụ, để tạo ra các nomogram lớn hơn để đạt được độ chính xác cao hơn, người lập bảng đồ thường chỉ bao gồm các phạm vi đo lường hợp lý và liên quan đến vấn đề. Nhiều bảng đồ bao gồm các đánh dấu hữu ích khác như nhãn tham chiếu và các vùng màu sắc. Tất cả những điều này cung cấp những dấu chỉ hữu ích cho người dùng.

Giống như thước trượt, nomogram (bảng đồ) là một thiết bị tính toán tương tự đồ họa. Cũng giống như thước trượt, độ chính xác của nó bị giới hạn bởi độ chính xác mà các đánh dấu vật lý có thể được vẽ, sao chép, quan sát và căn chỉnh. Khác với thước trượt, một công cụ tính toán đa dụng, nomogram được thiết kế để thực hiện một phép tính cụ thể với các bảng giá trị được tích hợp vào các thang đo của thiết bị. Nomogram thường được sử dụng trong các ứng dụng mà mức độ chính xác mà nó cung cấp là vừa đủ và hữu ích. Nói theo cách khác, nomogram có thể được sử dụng để kiểm tra một kết quả thu được từ phép tính chính xác hơn nhưng dễ mắc lỗi.
Các loại máy tính đồ họa khác - như biểu đồ chặn, biểu đồ tam tuyến và biểu đồ lục giác - đôi khi cũng được gọi là các bảng đồ nomogram. Những thiết bị này không đáp ứng định nghĩa của monogram như là một thiết bị tính toán đồ họa mà giải pháp được tìm ra thông qua việc sử dụng một hoặc nhiều đường đẳng phương tuyến.
Mô tả
sửaMột nomogram cho một phương trình ba biến thông thường có ba thang đo, mặc dù cũng có những nomogram chỉ có hai hoặc thậm chí cả ba thang đo phổ biến. Ở đây, hai thang đo đại diện cho các giá trị đã biết và giá trị thứ ba của thang đo là kết quả. Ví dụ đơn giản nhất đó là phương trình u1 + u2 + u3 = 0 cho ba biến u1, u2 và u3. Một ví dụ cho loại nomogram này được thể hiện ở bên phải, được chú thích với các thuật ngữ được sử dụng để mô tả các bộ phận của một nomogram.
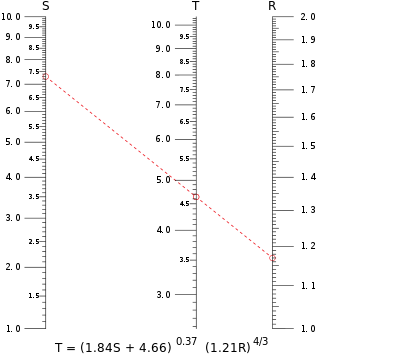
Các phương trình phức tạp hơn thỉnh thoảng có thể được thể hiện dưới dạng tổng của các hàm số ba biến. Ví dụ, nomogram Ở trên đầu của bài viết này có thể được xây dựng như một nomogram thang song song bởi vì nó có thể được biểu đạt dưới dạng một tổng sau khi lấy các lô-ga-rít ở cả hai đầu của phương trình.
Thang đo cho biến không xác định có thể nằm giữa hai thang đo khác hoặc bên ngoài chúng. Các giá trị đã biết của phép tính được đánh dấu trên thang đo cho các biến đó, và một đường thẳng được kẻ giữa những đánh dấu này. Kết quả được đọc trên thang đo cho biến không xác định tại điểm mà đường thẳng giao cắt thang đo đó. Các thang đo bao gồm 'các dấu tick' để chỉ những vị trí số chính xác, và chúng cũng có thể bao gồm các giá trị tham chiếu đã được gắn nhãn. Các tấm đo này có thể là tuyến tính, logarithmic, hoặc có mối quan hệ phức tạp hơn.
Ví dụ phương tuyến isopleth được thể hiện bằng màu đỏ trên nomogram tại đỉnh của bài viết này tính toán giá trị của T khi S = 7.30 và R =1.17. Đường phương tuyến isopleth chạy qua thang của T tại chỉ dưới 4.65; một hình ảnh được in ở độ phân giải cao trên giấy sẽ cho ra T = 4.64 chính xác tới ba chữ số thập phân. Lưu ý rằng bất kỳ biến số nào có thể được tính toán từ hai giá trị khác, một tính năng của nomogram đặc biệt hữu dụng trong các phương trình mà theo đó, một biến số không thể được phân tách theo cách đại số từ các giá trị biến khác.
Các thang thẳng rất hữu hiệu đối với các tính toán đơn giản, nhưng đối với các tính toán phức tạp hơn, việc sử dụng hoặc tích hợp các thang cong có thể là cần thiết. Các nomogram cho ba biến số trở lên có thể được xây dựng bằng cách tích hợp một lưới các thang đo cho hai trong số các biến số, hoặc bằng cách kết nối nhiều nomogram đơn lẻ vào trong một nomogram tổng hợp.
Ứng dụng
sửaNomogram được sử dụng trong nhiều tình huống khác nhau trong nhiều ngành nghề. Một thí dụ bao gồm:
- Ứng dụng ban đầu của d'Ocagne, tự động hóa các tính toán cắt và đắp phức tạp để loại bỏ đất trong quá trình xây dựng hệ thống đường sắt quốc gia Pháp. Đây là một bằng chứng quan trọng về mặt khái niệm, bởi vì các phép tính không hề tầm thường chút nào và kết quả của nó đã tiết kiệm đáng kể thời gian, công sức và tiền bạc.
- Thiết kế các kênh đào, đường ống và dây dẫn để điều phối dòng chảy của nước.
- Công trình của Lawrence Henderson, theo đó, các nomogram được sử dụng để liên hệ nhiều yếu tố của thông số máu. Đây là ứng dụng chính đầu tiên của nomogram tại Hoa Kỳ và cũng là nomogram y tế đầu tiên tại bất cứ đâu. [cần dẫn nguồn]
- Các ngành y học, ví dụ như dược học và ung thư học.[1]
- Các tính toán về đường đạn trước khi có hệ thống điều khiển phóng hoả, khi việc tính toán thời gian là rất quan trọng.
- Các tính toán trong xưởng máy móc, chuyển đổi kích thước từ bản vẽ kỹ thuật và thực hiện tính toán dựa trên kích thước và thuộc tính của vật liệu. Những nomogram thường bao gồm các đánh dấu cho các kích thước tiêu chuẩn và cho các bộ phận được sản xuất sẵn.
- Trong thống kê, các nomogram được sử dụng để tính các phép toán phức tạp các thuộc tính của phân phối và trong nghiên cứu về quản lý hoạt động bao gồm thiết kế các bài test kiểm tra kiểm soát chất lượng.
- Nghiên cứu các toán tử, để nhận lấy các kết quả cho một loạt các bài toán tối ưu hoá khác nhau.
- Trong lĩnh vực hóa học và kỹ thuật hóa học, nomogram được sử dụng để tổng hợp cả mối quan hệ vật lý chung và dữ liệu thực nghiệm cho các hợp chất cụ thể..
- Công nghệ hàng không, trong đó nomogram đã được sử dụng trong nhiều thập kỷ trong buồng lái của các loại máy bay khác nhau. Là một công cụ hỗ trợ điều hướng và kiểm soát chuyến bay, bảng đồ (nomogram) là các máy tính nhanh, nhỏ gọn và dễ sử dụng.
- Các tính toán thiên văn, cũng như các tính toán quỹ đạo sau khi phóng của Sputnik 1 bởi P.E. Elyasberg.[2]
- Mọi loại công việc kỹ thuật: Thiết kế điện cho các dây lọc và dây truyền tải, tính toán cơ học stress và tải, tính toán quang học, và còn nữa.
- Quân sự, khi các tính toán phức tạp cần phải được thực hiện ngay tại chiến trường và với mức độ tin cậy cao, không phụ thuộc vào các thiết bị điện tử.
- Địa chấn học, nơi mà Nomogram được phát triển để ước tính cường độ động đất và trình bày kết quả của các phân tích nguy cơ xác suất địa chấn.[3]
Các ví dụ
sửaĐiện trở song song/thấu kính mỏng
sửaNomogram dưới đây thực hiện phép tính toán:
Nomogram này là một công cụ thú vị bởi nó thực hiện một phép tính phi tuyến tính chỉ bằng cách sử dụng đường thẳng. Trong khi đường chéo có thang đo gấp lần lớn hơn các thang đo trục, các con số trên đó trùng khớp hoàn toàn với các số bên dưới hoặc về bên trái nó, và do đó nó có thể dễ dàng được tạo ra bằng cách vẽ một đường thẳng chéo trên tờ giấy đồ thị.
A và B được truy nhập trên các thang đo trục hoành và trục tung. Kết quả được đọc ra từ thang đo chéo. Bởi nó tỷ lệ với trung bình điều hoà của cả A và B, công thức này có một số áp dụng nhất định. Ví dụ, đó chính là công thức điện trở song song trong điện tử học, và phương trình thấu kính mỏng trong quang học.
Trong ví dụ, đường màu đỏ thể hiện rằng, các điện trở song song 56 và 42 Ohm có điện trở tổng là 24 Ohm. Nó cũng thể hiện rằng, một vật thể ở khoảng cách 56 cm từ một thấu kính với tiêu cự 24 cm sẽ tạo ra một hình ảnh thực có khoảng cách 42 cm.
Tính toán test kiểm tra Chi-square (Chi bình phương)
sửaNomogram bên dưới có thể được sử dụng để thực hiện một phép ước lượng các giá trị cần thiết khi làm một phép thử xác suất thống kê quen thuộc, test kiểm tra Chi bình phương của Pearson. Nomogram này thể hiện việc sử dụng các thang đường cong với mật độ gradient không đồng đều.
Biểu thức liên quan là:
Thang đo dọc theo phần đỉnh được chia cho năm phạm vi giá trị quan sát khác nhau: A, B, C, D và E. Giá trị quan sát được tìm thấy ở một trong các phạm vi này, và dấu tick kiểm được sử dụng trên thang đo đó nằm ngay phía trên giá trị đó. Sau đó, thang đo cong được sử dụng cho giá trị dự kiến được chọn dựa trên phạm vi. Ví dụ: giá trị được quan sát là 9 sẽ sử dụng dấu tick kiểm phía trên số 9 trong phạm vi A, và thang đo cong A sẽ được sử dụng cho giá trị dự kiến. Giá trị được quan sát là 81 sẽ sử dụng dấu tick kiểm trên 81 trong phạm vi E và thang đo cong E sẽ được sử dụng cho giá trị dự kiến. Điều này cho phép kết hợp năm biểu đồ nomogram khác nhau vào một đồ thị duy nhất.
Theo đó, đường màu xanh dương diễn đạt phép tính của:
(9 − 5)2 / 5 = 3.2
và đường màu đỏ diễn đạt phép tính của:
(81 − 70)2 / 70 = 1.7
Khi thực hiện thử nghiệm, điều chỉnh của Yates cho tính liền mạch thường được áp dụng, và đơn giản chỉ là trừ đi 0.5 từ các giá trị quan sát. Một nomogram thực hiện thử nghiệm với sự hiệu chỉnh của Yates có thể được xây dựng một cách đơn giản bằng cách di chuyển mỗi "thang đo quan sát" một nửa đơn vị sang bên trái, để các độ chia 1.0, 2.0, 3.0, ... được đặt tại những giá trị 0.5, 1.5, 2.5, ... xuất hiện trên biểu đồ hiện tại.
Đánh giá nguy cơ thực phẩm
sửaMặc dù bảng nomogram đại diện cho mối quan hệ toán học, nhưng không phải tất cả đều dựa trên toán học. Nomogram sau này được phát triển bằng đồ họa để đạt được các kết quả cuối cùng thích hợp, có thể được xác định dễ dàng bằng tích của các mối quan hệ của chúng theo đơn vị chủ quan thay vì theo số lượng. Việc sử dụng các trục không song song cho phép tích hợp các mối quan hệ phi tuyến tính vào mô hình.
Các số trong ô vuông biểu thị các trục yêu cầu đầu vào sau khi được đánh giá thích hợp.
Cặp Momogram ở đầu hình xác định xác suất xảy ra và tính sẵn có, sau đó được tích hợp vào nomogram đa tầng ở phía dưới.
Các đường 8 và 10 là 'đường nối' hoặc 'đường trục' và được sử dụng để chuyển đổi giữa các giai đoạn của nomogram hợp chất.
Cặp thang đo song song cuối cùng (12) không phải là một nomogram như vậy, mà là các thang đo chuyển đổi điểm số rủi ro (11, từ rất thấp đến cực cao) thành tần suất lấy mẫu để giải quyết các khía cạnh an toàn và các khía cạnh 'bảo vệ người tiêu dùng' tương ứng. Giai đoạn này đòi hỏi sự ủng hộ chính trị có cân nhắc giữa chi phí và rủi ro. Ví dụ sử dụng tần suất tối thiểu ba năm cho mỗi tần suất, tuy nhiên với đầu cuối rủi ro cao của các thang đo khác nhau cho hai khía cạnh, cho hai tần suất khác nhau, nhưng đều phải tuân theo một tần suất lấy mẫu tối thiểu chung cho tất cả khía cạnh của tất cả các loại thực phẩm ít nhất một lần mỗi ba năm.
Bảng nomogram đánh giá rủi ro này được phát triển bởi UK Public Analyst Service của Vương quốc Anh với nguồn tài trợ từ UK Food Standards Agency để sử dụng như một công cụ chỉ dẫn tần suất thích hợp của việc lấy mẫu và phân tích thực phẩm cho mục đích kiểm soát thực phẩm chính thức, dự định cho sử dụng đánh giá tất cả các vấn đề tiềm ẩn với mọi loại thực phẩm, mặc dù vẫn chưa được áp dụng.
Một số bảng đồ nomogram gọn và tiện dụng
sửaSử dụng một cây thước thẳng, ta có thể dễ dàng đọc được biến số còn bị thiếu của định lý sin hoặc nghiệm của các phương trình bậc hai hoặc bậc ba.[4]
-
Nomogram cho định luật sin
-
Nomogram để giải phương trình bậc hai x^2+px+q=0
-
Nomogram để giải phương trình bậc ba x^3+px+q=0
Xem thêm
sửaChú thích và Tham khảo
sửaBài viết này có một danh sách các nguồn tham khảo, nhưng vẫn chưa đáp ứng khả năng kiểm chứng được bởi thân bài vẫn còn thiếu các chú thích trong hàng. (November 2013) |
- ^ Ha, Yun-Sok; Kim, Tae-Hwan (1 tháng 1 năm 2018), Ku, Ja Hyeon (biên tập), “Chapter 30 - The Surveillance for Muscle-Invasive Bladder Cancer (MIBC)”, Bladder Cancer (bằng tiếng Anh), Academic Press, tr. 553–597, doi:10.1016/b978-0-12-809939-1.00030-8, ISBN 978-0-12-809939-1, truy cập ngày 11 tháng 11 năm 2022
- ^ Yu.A.Mozzhorin Memories Lưu trữ 2007-10-18 tại Wayback Machine at the website of Russian state archive for scientific-technical documentation
- ^ Douglas, John; Danciu, Laurentiu (8 tháng 11 năm 2019). “Nomogram to help explain probabilistic seismic hazard”. Journal of Seismology (bằng tiếng Anh). 24 (1): 221–228. Bibcode:2020JSeis..24..221D. doi:10.1007/s10950-019-09885-4. ISSN 1573-157X.
- ^ Szalkai, Istvan; Balint, Roland (28 tháng 12 năm 2017). “Nomograms for the quadratic and cubic equations (in Hungarian)” (PDF). Haladvány Kiadvány. 2017.
Đọc thêm
sửa- D.P. Adams, Nomography: Theory and Application, (Archon Books) 1964.
- H.J. Allcock, J. Reginald Jones, and J.G.L. Michel, The Nomogram. The Theory and Practical Construction of Computation Charts, 5th ed., (London: Sir Isaac Pitman & Sons, Ltd.) 1963. (1st edition 1932)
- S. Brodestsky, A First Course in Nomography, (London, G. Bell and Sons) 1920.
- D.S. Davis, Empirical Equations and Nomography, (New York: McGraw-Hill Book Co.) 1943.
- M. d'Ocagne: Traité de Nomographie, (Gauthier-Villars, Paris) 1899.
- M. d'Ocagne: (1900) Sur la résolution nomographique de l'équation du septième degré. Comptes rendus (Paris), 131, 522–524.
- R.D. Douglass and D.P. Adams, Elements of Nomography, (New York: McGraw-Hill) 1947.
- R.P. Hoelscher, et al., Graphic Aids in Engineering Computation, (New York: McGraw-Hill) 1952.
- L. Ivan Epstein, Nomography, (New York: Interscience Publishers) 1958.
- L.H. Johnson, Nomography and Empirical Equations, (New York: John Wiley and Sons) 1952.
- M. Kattan and J. Marasco. (2010) What Is a Real Nomogram?, Seminars in oncology, 37(1), 23–26.
- A.S. Levens, Nomography, 2nd ed., (New York: John Wiley & Sons, Inc.) 1959.
- F.T. Mavis, The Construction of Nomographic Charts, (Scranton, International Textbook) 1939.
- E. Otto, Nomography,(New York: The Macmillan Company) 1963.
- H.A. Evesham The History and Development of Nomography, (Boston: Docent Press) 2010. ISBN 9781456479626
- T.H. Gronwall, R. Doerfler, A. Gluchoff, and S. Guthery, Calculating Curves: The Mathematics, History, and Aesthetic Appeal of T. H. Gronwall's Nomographic Work, (Boston: Docent Press) 2012. ISBN 9780983700432
Các liên kết ngoài
sửa- Weisstein, Eric W., "Nomogram" từ MathWorld.
- The Art of Nomography mô tả việc thiết kế các nomogram sử dụng hình học, các determinant, và các phép chuyển đổi.
- The Lost Art of Nomography là một bài báo tạp chí toán học khảo sát ngành nomography.
- Nomograms for Wargames một ứng dụng thú vị của nomogram.
- PyNomo – phần mềm mã nguồn mở cho phép xây dựng các nomogram.
- Java Applet Lưu trữ 2009-09-24 tại Wayback Machine khởi tạo các nomogram đơn giản.
- Nomograms for visualising relationships between three variables - video và các slide của cuộc hội thoại được mời bởi Jonathan Rougier cho useR!2011.