Không gian moduli
Trong toán học, đặc biệt là hình học đại số, một không gian mo-đu-li (hay không gian moduli) là một không gian hình học (thường là một lược đồ hoặc một chùm đại số) có các điểm đại diện cho các đối tượng hình học, hoặc các lớp đẳng cấu của các đối tượng hình học đó. Các không gian như vậy thường là giải pháp cho các vấn đề phân loại hoặc các vấn đề cực đại, cực tiểu.
Thuật ngữ moduli mang nghĩa gần với tham số: ta tham số hóa các đối tượng bằng các điểm trong một không gian.
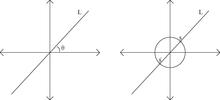
Ví dụ cơ bản
sửaKhông gian xạ ảnh và các Grassmann
sửaKhông gian xạ ảnh Pn là không gian moduli của các đường thẳng trong R n +1 đi qua gốc. Tương tự, không gian xạ ảnh phức là không gian moduli của các đường thẳng phức trong Cn+1 đi qua gốc.
Một đa tạp Grassmann G(k,V) của không gian vectơ V trên một trường F là không gian moduli của tất cả các không gian con tuyến tính k chiều của V.
Lược đồ Hilbert
sửaLược đồ Hilbert Hilb(X) là một lược đồ moduli. Mọi điểm đóng của Hilb(X) tương ứng với một lược đồ con đóng của lược đồ X.
Xem thêm
sửaCông cụ xây dựng
sửa- Lược đồ Hilbert
- Lược đồ Quot
- Lý thuyết biến dạng
- Thương GIT
- Tiêu chuẩn Artin, tiêu chuẩn chung để xây dựng các không gian moduli như các chùm đại số từ các hàm tử moduli
Không gian Moduli
sửa- Moduli của các đường cong đại số
- Chùm moduli của các đường cong elliptic
- Đường cong mo-đu-la
- Hàm tử Picard
- Moduli các bó nửa ổn định trên một đường cong
- Không gian moduli Kontsevich
- Moduli các bó nửa ổn định
Tham khảo
sửa- Grothendieck, Alexander (1960–1961). “Techniques de construction en géométrie analytique. I. Description axiomatique de l'espace de Teichmüller et de ses variantes” (PDF). Séminaire Henri Cartan 13 No. 1, Exposés No. 7 and 8.
- Mumford, David, Lý thuyết bất biến hình học. Er Quaynisse der Mathematik und ihrer Grenzrosse, Neue Folge, Band 34 Springer-Verlag, Berlin-New York 1965 vi + 145 pp MR0214602 02146020214602
- Mumford, David; Fogarty, J.; Kirwan, F. Lý thuyết bất biến hình học. Ấn bản thứ ba. Er Quaynisse der Mathematik und ihrer Grenzrosse (2) (Kết quả trong Toán học và các lĩnh vực liên quan (2)), 34. Springer-Verlag, Berlin, 1994. xiv + 292 trang. MR1304906 ISBN 3-540-56963-4
- Papadopoulos, Athanase, chủ biên. (2007), Sổ tay lý thuyết Teichmüller. Tập I, IRMA Các bài giảng về Toán học và Vật lý lý thuyết, 11, Hiệp hội toán học châu Âu (EMS), Zürich, doi:10.4171/029, ISBN 978-3-03719-029-6, MR2284826 22848262284826
- Papadopoulos, Athanase, chủ biên. (2009), Sổ tay lý thuyết Teichmüller. Tập II, IRMA Các bài giảng về Toán học và Vật lý lý thuyết, 13, Hiệp hội toán học châu Âu (EMS), Zürich, doi:10.4171/055, ISBN 978-3-03719-055-5, MR2524085 25240852524085
- Papadopoulos, Athanase, chủ biên. (2012), Sổ tay lý thuyết Teichmüller. Tập III, IRMA Các bài giảng về Toán học và Vật lý lý thuyết, 17, Hiệp hội toán học châu Âu (EMS), Zürich, doi:10.4171/103, ISBN 978-3-03719-103-3.
- Deligne, Pierre; Mumford, David (1969). “The irreducibility of the space of curves of given genus” (PDF). Publications Mathématiques de l'IHÉS. 36: 75–109. doi:10.1007/bf02684599.
- Harris, Joe; Morrison, Ian (1998). Moduli of Curves. Graduate Texts in Mathematics. 187. New York: Springer Verlag. doi:10.1007/b98867. ISBN 978-0-387-98429-2. MR 1631825.
- Katz, Nicholas M; Mazur, Barry (1985). Arithmetic Moduli of Elliptic Curves. Annals of Mathematics Studies. 108. Princeton University Press. ISBN 978-0-691-08352-0. MR 0772569.
- Faltings, Gerd; Chai, Ching-Li (1990). Degeneration of Abelian Varieties. Ergebnisse der Mathematik und ihrer Grenzgebiete. 22. With an appendix by David Mumford. Berlin: Springer-Verlag. doi:10.1007/978-3-662-02632-8. ISBN 978-3-540-52015-3. MR 1083353.
- Viehweg, Eckart (1995). Quasi-Projective Moduli for Polarized Manifolds (PDF). Springer Verlag. ISBN 978-3-540-59255-6.
- Simpson, Carlos (1994). “Moduli of representations of the fundamental group of a smooth projective variety I” (PDF). Publications Mathématiques de l'IHÉS. 79: 47–129. doi:10.1007/bf02698887.
- Maryam Mizakhani (2007) "Đường trắc địa đơn và thể tích Weil-Petersson của không gian moduli các bề mặt Riemann có biên" Inventiones mathematicae, volume 167, tr. 179–222
Liên kết ngoài
sửa- Lurie, J. (2011). “Moduli Problems for Ring Spectra”. Proceedings of the International Congress of Mathematicians 2010 (ICM 2010). tr. 1099–1125. doi:10.1142/9789814324359_0088.