Cây (cấu trúc dữ liệu)

Trong khoa học máy tính, cây là một cấu trúc dữ liệu được sử dụng rộng rãi gồm một tập hợp các nút (tiếng Anh: node) được liên kết với nhau theo quan hệ cha-con. Cây trong cấu trúc dữ liệu đầu tiên là mô phỏng (hay nói cách khác là sự sao chép) của cây (có gốc) trong lý thuyết đồ thị. Hầu như mọi khái niệm trong cây của lý thuyết đồ thị đều được thể hiện trong cấu trúc dữ liệu. Tuy nhiên cây trong cấu trúc dữ liệu đã tìm được ứng dụng phong phú và hiệu quả trong nhiều giải thuật. Khi phân tích các giải thuật trên cấu trúc dữ liệu cây, người ta vẫn thường vẽ ra các cây tương ứng trong lý thuyết đồ thị.

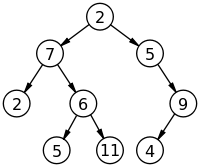
Các nút

Một nút có thể chứa một giá trị, một điều kiện, một cấu trúc dữ liệu riêng biệt hoặc chính một cây. Mỗi nút trong một cây có thể không có hoặc có một số nút con, các nút con có mức cao hơn nó (theo quy ước khác với cây tự nhiên, cây trong cấu trúc dữ liệu phát triển từ trên xuống). Một nút có con được gọi là nút cha của các nút con. Một nút có nhiều nhất một nút cha.

Nút gốc

Trong mỗi cây có một nút đặc biệt được gọi là nút gốc (hay nói đơn giản là gốc). Nút gốc là nút duy nhất không có nút cha. Nút gốc là nơi khởi đầu của nhiều giải thuật trên cây. Tất cả các nút khác được nối về nút gốc bằng một đường đi qua các cạnh hay các liên kết

Các nút lá

Các nút không có nút con được gọi là nút lá hay gọi đơn giản là lá.

Các nút trong (nút nhánh)

nút trong của một cây là nút trên cây có ít nhất một con, nghĩa là các nút không phải là lá. Các khái niệm về mức của mỗi nút, chiều cao của cây được định nghĩa giống như cây trong lý thuyết đồ thị.

Cây con

Một cây con là một bộ phận của cấu trúc dữ liệu cây mà tự nó cũng là một cây. Một nút bất kỳ trong cây T, cùng với các nút dưới nó tạo thành một cây con của T.

Cây trong lý thuyết đồ thị

Trong lý thuyết đồ thị, một cây là một đồ thị liên thông và không có chu trình. Cây như vậy còn được gọi là cây tự do. Một cây có gốc là một cây tư do, trong đó có một đỉnh được chọn làm gốc và các cạnh được định hướng là hướng của các đường đi đơn ra khỏi gốc tới các đỉnh khác. Trong trường hợp này, hai đỉnh bất kỳ được nối với nhau bao hàm chúng có qua hệ cha-con. Một đồ thị không chu trình với nhiều thành phần liên thông được gọi là một rừng.

Cây sắp thứ tự

Có hai dạng cấu trúc cơ sở của cây là cây không thứ tự và cây có thứ tự. Một cây không thứ tự là cây có cấu trúc cây, trong đó giữa các con của một nút, không có thứ tự nào. Một cây, trong đó các con của một nút tuân theo một thứ tự xác định được gọi là cây có thứ tự. Các cây có thứ tự có nhiều ứng dụng sâu sắc trong cấu trúc của cây. Cây tìm kiếm nhị phân là một cây sắp thứ tự điển hình.

Cây tổng quát và cây nhị phân

Các cây trong đó mỗi nút có thể có nhiều hơn hai con được gọi là cây tổng quát, các cây trong đó mỗi nút có không quá hai con được gọi là cây nhị phân.

Biểu diễn cây

Có nhiều phương pháp biểu diễn cây. Cách thường dùng nhất là biểu diễn mỗi nút như một dữ liệu kiểu bản ghi, mỗi nút chứa các con trỏ tới các con hoặc cha của nó, hoặc cả hai. Cây cũng có thể biểu diễn bằng các mảng cùng với quan hệ giữa các vị trí trong mảng.

Biểu diễn bằng các nút với các con trỏ

Mỗi nút là một dữ liệu kiểu bản ghi với ba trường: Một trường thường gọi là INFOR, chứa thông tin lưu trữ tại nút đó. Thông tin này có thể chỉ là một số, một ký tự, cũng có thể là một tập hợp dữ liệu rất phức tạp. Hai trường LLINK và RLINK chứa các liên kết trái và phải. Nếu cây là cây nhị phân, LLINK trỏ tới con trái của nút, RLINK trỏ tới con phải của nút. Nếu cây là cây tổng quát, LLINK trỏ tới con cực trái và RLINK trỏ tới em kế cận phải của nút đó. Do đó danh sách các nút biểu diễn một cây tổng quát, khi được xem là biểu diễn của cây nhị phân sẽ cho một cây nhị phân. Cây nhị phân này được gọi là cây nhị phân tương đương với cây tổng quát ban đầu.

Biểu diễn cây nhị phân bằng mảng

Cây nhị phân mà mỗi đỉnh trong có đúng hai con được gọi là cây nhị phân đầy đủ (full binary tree)
Cây nhị phân đầy đủ mà tất cả các lá có cùng một mức được gọi là cây nhị phân hoàn chỉnh (perfect binary tree). Một số tài liệu gọi cây loại này là cây đầy đủ.
Cây nhị phân mà mỗi đỉnh của nó đã có con phải thì cũng có con trái được gọi là cây nhị phân gần hoàn chỉnh (almost complete binary tree). (Định nghĩa này sai, theo đó cây suy biến lệch trái cũng là gần hoàn chỉnh?)
Ta có thể dùng một mảng gồm $2^{h+1}-1$ phần tử để biểu diễn cây nhị phân, bằng cách lần lượt lưu trữ thông tin của mỗi nút vào mảng theo thứ tự từ trên xuống dưới, từ trái sang phải. Khi đó con trái của nút thứ i là phần tử thứ 2*i, con phải là phần tử thứ 2*i+1. Cha của phần tử thứ i là phần tử thứ int(i/2).Ta gán giá trị Null cho các vị trí còn thiếu.
Một cách khác, dùng một mảng hai chiều trong dòng thứ nhất ghi các thông tin của nút, dòng thứ hai ghi chỉ số của nút cha của nút đó với dấu + nếu nút hiện tại là con trái, với dấu - nếu nút hiện tại là con phải của nút cha.

Các phương pháp duyệt cây

Duyệt một cây là một trình tự làm việc với các nút trong cây, trình tự này giống như một chuyến đi qua các nút trên cây theo các liên kết cha-con, bắt đầu từ nút gốc. Các giải thuật duyệt khác nhau về thứ tự "viếng thăm" giữa một nút cha và các nút con.